ScienceBooks
1강 혼돈의 양자 스핀: 이성빈 카이스트 교수 1편 본문
한국 물리학회 교육 위원회가 주관하고 (주)사이언스북스가 후원하는 「물리 어벤져스 2019」가 시작되었습니다. 「물리 어벤져스 2019」의 첫 강연은 지난 5월 24일(금)에 있었습니다. 양자 역학을 무기로 응집 물질 물리학을 연구하는 이성빈 카이스트 교수가 첫 강연자로 나서 주셨습니다. 앞으로 황정아 천문연 선임 연구원, 임혜인 숙명여대 교수, 윤진희 인하대 교수 등 한국을 대표하는 여성 물리학자들의 강연이 9월 말까지 펼쳐질 텐데, 사이언스북스 블로그에서 이 강연들의 스케치 기사를 연재할 예정입니다. 프리랜서 작가로 활약하고 있는 신연선 작가가 이 스케치 기사를 맡아 줄 겁니다. 많은 관심 가져 주시면 좋겠습니다.
물리 어벤져스 2019 스케치
1강 혼돈의 양자 스핀: 이성빈 카이스트 교수 1편

이성빈 카이스트 물리학과 교수님은 일본의 도쿄 공업 대학, 미국의 캘리포니아 주립 대학교 샌타바버라 캠퍼스를 졸업하고 현재 카이스트 물리학과 조교수로 활약하고 있는 양자 물리학 전문가입니다. 카이스트가 야심 차게 스카우트해 왔다는 소문이 도는 젊은 물리학자죠. 전공은 응집 물질 물리학 이론인데요. 응집 물질 물리 이론 중에서도 양자 자성 및 새로운 양자 상태를 연구하고 있습니다. 현대 물리학의 핵심이라고도 할 수 있는 응집 물질 물리학이란 무엇일까요?
지난 5월 24일(금), 「물리 어벤져스 2019」 첫 번째 시간은 “혼돈의 양자 스핀: 무질서에 의한 질서”라는 제목으로 이성빈 교수님과 함께 다소 생소하게 들릴 수 있는 응집 물리학, 그중에서도 전자의 스핀을 살펴보았습니다. 강연과 질의응답 등의 진행 및 사회는 한국 물리학회 교육 위원회 위원장을 맡고 계신 홍석철 고려 대학교 물리학과 교수님이 맡으셨습니다. 전자의 스핀이 어떻게 쩔쩔매게 되는지를 파헤쳐 보고, 그 안에서 무질서에 의해 새로운 질서가 생기는 현상까지도 이해하는 시간이었습니다.
물리하는 사람들의 '존재의 이유'
이성빈 교수님은 “제목을 멋지게 지어 보려고 해 봤다.”라며 가벼운 농담으로 강연을 시작했습니다. “양자 스핀이 왜 혼돈 상태에 있으며, 그 안에서 무질서에 의해 어떤 질서가 나타날 수 있는지 말씀드리겠다.”라며 우선 교수님이 어떻게 물리를 만나고, 언제 물리에 매료되었는지에 대한 이야기로 강연의 문을 열었습니다.
“물리 하는 사람들이라고 하면 어떤 사람들이 떠오르세요? 여기 아주 유명하신 분들을 나열해 봤습니다. 모두 아시는 뉴턴(Isaac Newton)이 있겠고요. ‘맥스웰 방정식’으로 전자기학의 태초가 된 제임스 클러크 맥스웰(James Clerk Maxwell)이 있습니다. 또 알베르트 아인슈타인(Albert Einstein)도 있죠. 그다음 양자 역학의 시초라 할 에르빈 슈뢰딩거(Erwin Schrodinger)가 있고, 가장 최근의 물리학자로 스티븐 호킹(Stephen William Hawking)이 있습니다. 이분들은 누구도 의심하지 않는 물리학자들인데요. 모든 물리학자가 이렇게 유명하진 않죠. 저처럼 잘 모르는 사람들도 있기 때문에 (웃음) 제가 어떤 식으로 물리를 하게 됐는지부터 말씀드리겠습니다.”
중학생 때 칼 세이건의 동명 소설 『콘택트』를 원작으로 한 SF 영화 「콘택트」를 흥미롭게 봤다는 이성빈 교수님은 “이걸 보면서 존재의 이유를 많이 생각했던 기억이 난다.”라고 말했습니다. 어쩌면 교수님이 물리학을 만난 최초의 순간이 아닐까 싶은데요. 우주와 생명의 근원을 깊이, 더 깊이 파고드는 물리학과 ‘존재의 이유’를 생각한 중학생 이성빈의 모습을 상상하게 하는 대목이었습니다. 이어 고등학생이 된 후 이성빈 교수님은 ‘SETI@HOME’을 만나게 되는데요. ‘SETI@HOME’은 SETI 프로그램의 일환으로 인터넷에 연결된 컴퓨터들을 이용해 외계 지적 생명체를 탐구하는 프로젝트이지요. 미국의 캘리포니아 대학교 버클리 캠퍼스에서 1999년 5월 17일 일반에 공개했고, 현재 국내에서는 이명현 박사님이 한국 책임자를 지내고 계시기도 합니다.

“‘SETI@HOME’이 1999년에 나왔어요. 컴퓨터만 켜놓으면 도움이 되겠구나, 라고 생각해서 가끔 컴퓨터를 켜서 시그널을 보곤 했습니다. 무슨 말인지는 전혀 몰랐지만 말이죠. (웃음) 그밖에 과학 잡지 《과학동아》나 《뉴턴》도 재미있게 봤어요. 특히 이런 잡지에 자주 등장하는 내용이 ‘우주론’이었거든요. 사춘기 때 존재의 이유에 대해 많이 생각하잖아요. 저도 여기에 매력을 많이 느꼈어요. 블랙홀과 화이트홀, 웜홀을 따라 시간 여행을 할 수 있다 하는 내용을 엄청나게 읽었습니다.”
‘우주의 신비를 깨우치고 싶다.’는 생각에 막연하게 관심을 갖고 과학책을 탐독하고, 나아가 물리학을 공부해 보면 좋겠다고 생각한 이성빈 교수님은 이윽고 도쿄 공대 물리학과에 진학하게 됩니다. 고전 역학과 전자기학, 양자 역학, 통계 역학 등을 배우는 가운데 특히 ‘전자 궤도와 전자의 구름’에 흥미를 느꼈던 당시의 기억을 전했습니다.
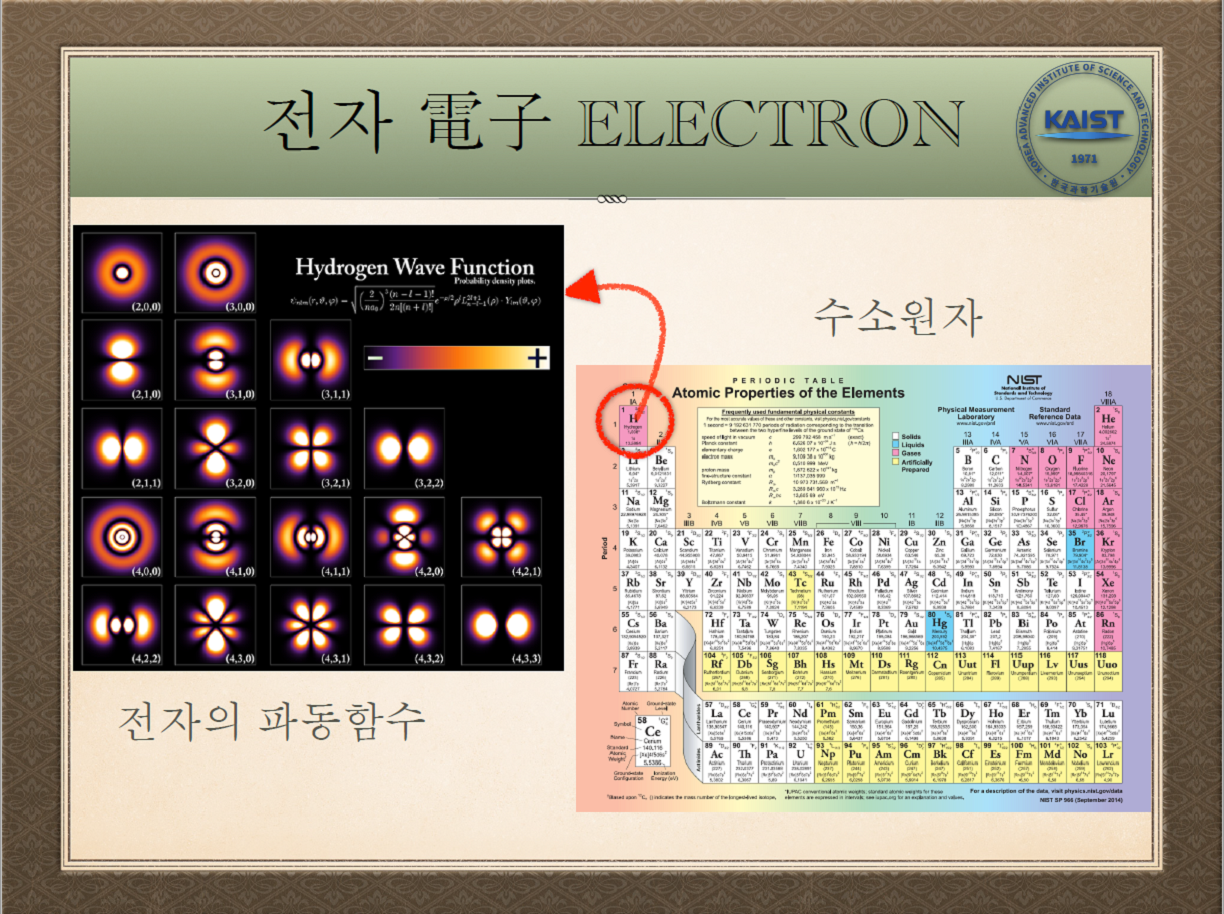
“여기 주기율표가 있는데요. 가장 처음 나오는, 전자가 하나 있는 수소 원자(H)의 경우 수소 원자의 전자의 파동 함수가 어떻게 되는가에 대해서는 우리가 정확히 풀 수 있습니다. (위 이미지의) 밝은 빛이 나는 전자가 구름으로 많이 모여 있다고 확률적으로 해석을 해요. ‘수소 원자의 파동 함수(Hydrogen Wave Function)’라는 것을 풀 수 있는 거죠.”
이어 대학교 학부생 이성빈이 처음 양자 역학을 만난 순간이 됐습니다. 현재 카이스트 대학원에서 양자 역학 강의를 진행하고 있는 이성빈 교수님도 얼굴에 미소를 띠고“저 역시 양자 역학을 배우면서, 배우면 배울수록 ‘내가 이해하고 있는 것이 맞나?’라는 생각이 늘 들었다.”라고 말하며 양자 역학이 어렵다는 사실에 공감하기도 했습니다. 아인슈타인은 “신은 주사위를 던지지 않는다.”라며 양자 역학을 끝까지 거부했지만 “불확정성의 원리(Uncertainty Principle)가 요즘은 당연하게 받아들여지고 있다.”라는 설명도 이어졌습니다.
전자라는 입자는 파동의 성질을 갖는다. 달리 말하면 전자는 입자이면서 파동이라는 말이다. 하지만 입자성과 파동성을 동시에 보일 수는 없다. 이들은 상보적 관계에 있기 때문이다. 하이젠베르크의 불확정성 원리에서는 물체의 위치와 운동량이 상보적이라 볼 수 있다. 즉 전자의 위치와 운동량을 동시에 정확히 결정할 수 없다는 뜻이다. (김상욱, 『김상욱의 양자 공부』, 133-134쪽)
“즉 파동과 입자가 이중성이 있고, 우리가 관측하는 입자의 위치나 운동량 자체는 100퍼센트 정확하게 관측할 수 없다는 게 불확정성의 원리입니다. 당연히 수식으로 설명할 수가 있어요. 우리가 관측하는 순간 뭔가 일이 일어난다는 양자 역학의 철학인데요. 이 불확정성의 원리를 아래 수식을 조금 이용하면 정확히 볼 수 있습니다.”

전자는 격자를 따라 흐르고
앞서 잠깐이나마 전자의 파동 함수를 엿보았습니다. 이성빈 교수님은 이제 전자를 조금 더 자세히 살펴봅니다. 이성빈 교수님은 “전자가 어떤 식으로 흘러가는지”를 살펴보려면 아주 쉽게는 ‘상전이’를 떠올릴 수 있다며 가볍게 전자의 흐름을 설명했습니다.
“얼음을 끓이면 물이 되고, 물을 끓이면 수증기가 된다, 이것을 상전이(phase transition)라고 합니다. 상이 바뀐다는 의미인데요. 이때 얼음을 보면 육각 격자를 관찰할 수 있어요. 이 같은 격자 안에서 전자가 어떻게 흘러가는가, 이것을 연구하는 게 예를 들면 반도체 산업의 기반이 되고요. 결론적으로 전자가 어떻게 흘러가는가를 공부하는 것이 응집 물질학입니다. 이때 전자의 스핀은 1/2라는 숫자를 가지는데, 이 숫자는 무엇을 의미할까요? 가령 냉장고에 자석이 붙는 것도 전자의 스핀이 있기 때문입니다. 철(F)과 산소(O)를 조합하면 철산화물(Fe₂O₃)이 되는데요. 철산화물로 이루어진 자석은 격자 구조를 갖고 있습니다. 그 안에서 스핀이 한쪽으로 정렬되어 있기 때문에 자성을 띄고, 이것이 냉장고에 붙을 수 있게 되는 것이죠. 저희는 이러한 전자의 돌아다님을 연구합니다.”
격자. 이성빈 교수님은 전자의 흐름을 연구할 때 격자가 중요한 역할을 한다고 말했습니다. “격자가 어떻게 생겼는지에 따라 연필심이 되기도 하고, 다이아몬드가 되기도 하기 때문”이라는 이성빈 교수님은 재미있는 이미지를 보여 주었습니다.
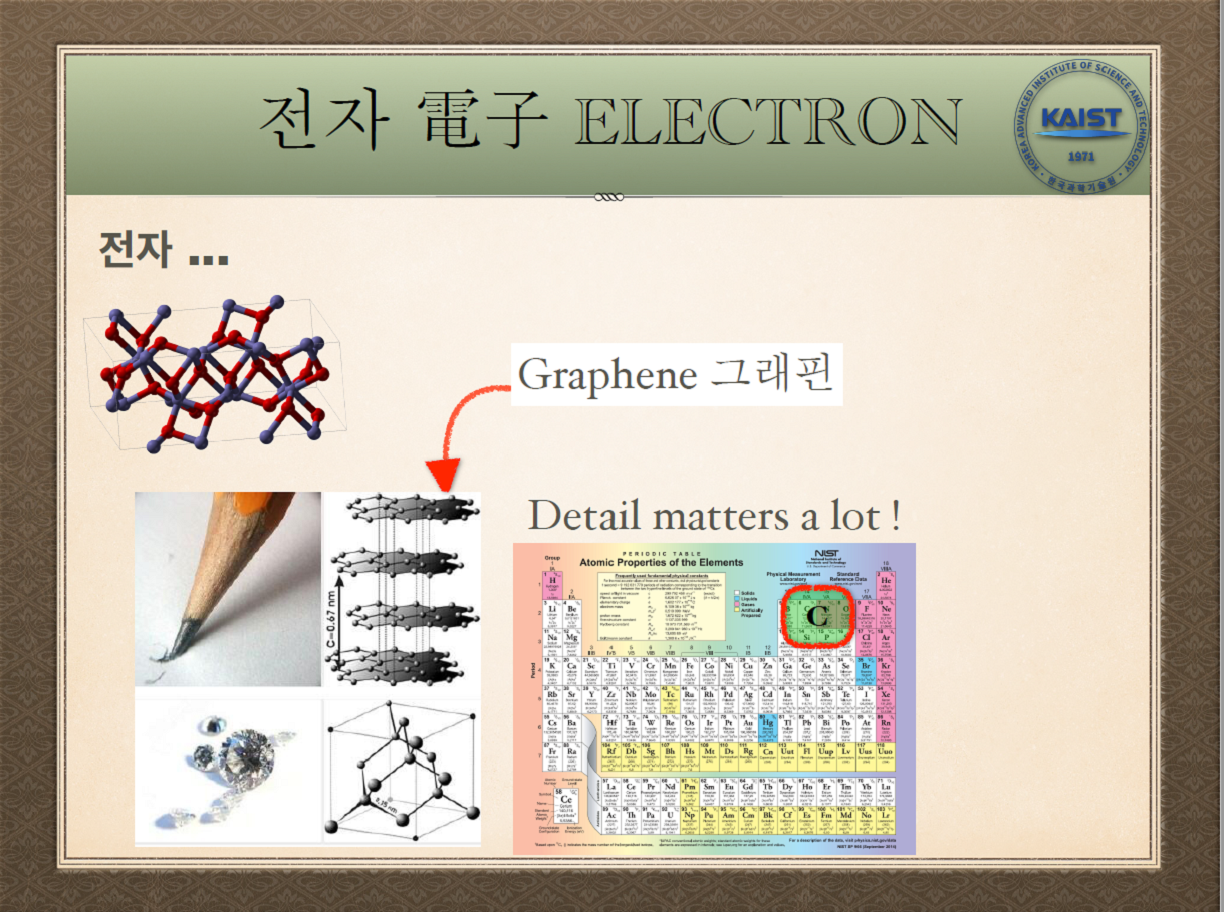
“연필과 다이아몬드는 모두 탄소(C)로 이루어져 있는데요. 격자가 어떻게 생겼느냐에 따라 큰 차이가 나죠. 우리가 연필심을 아주 살짝 떼어 내면 그래핀(Graphene)이라는 육각 구조가 층층으로 쌓여 있는 것을 관찰할 수 있는데요. 다이아몬드는 연필과 다른 격자예요. 디테일이 중요한 겁니다. (웃음) 육각 격자로 층층이 생겼느냐, 다이아몬드 격자로 생겼느냐에 따라 큰 차이가 나요.”
2004년 연필에서 ‘그래핀’을 떼어 내는 데 성공한 가임(A. K. Geim)과 노보셀로프(K. S. Novoselov)는 2010년 노벨 물리학상을 받기도 했습니다. 당시 노벨상 위원회는 “그래핀이라는 완전히 새로운 종류의 물질”을 발견한 이들의 “뛰어난 업적”을 재확인하며 다음과 같이 말하기도 했습니다.
“오랫동안 흑연이 육각 탄소층으로 되어 있다는 것이 잘 알려져 있었고, 그래핀에서의 전자 거동은 이미 1947년 필립 월러스가 이론적으로 밝힌 바 있습니다. 그러나 그래핀을 단층으로 분리하여 그 전기적 특성을 측정할 수 있으리라고 믿는 과학자는 거의 없었습니다. 따라서 올해의 노벨상 수상자인 안드레 가임과 콘스탄틴 노보셀로프가 2004년 10월 동료들과 함께 발표한 연구 결과는 놀라움 그 자체였습니다. 그들은 흔한 사무용품인 접착 테이프를 이용한 매우 창조적인 방법으로 단일 탄소층을 분리해 적절한 표면 위에 전이시키는 데 성공했습니다. 그들은 특별한 현미경을 통해 이들이 단원자층으로 되어 있음을 보였으며, 적당한 모양으로 이를 가공하고 전극을 붙여 전기적 특성을 측정하기도 하였습니다. 이후 오늘의 노벨상 수상자뿐 아니라 많은 연구진들이 새로운 탄소 물질의 놀라운 특성들을 연구하고 있습니다.”(노벨상 위원회 노벨상 수상 이유에서)
흥미로운 것은 2차원의 격자 구조, 3차원의 격자 구조가 몇 개 있는지를 수학적으로 구할 수 있다는 점이었습니다. 이성빈 교수님은 언뜻 아름다운 직물의 샘플을 모아둔 것 같은 격자 구조 이미지들을 보여 주며 물리학의 세계를 선명하게 인식시켰습니다.
“가령 2차원의 격자 구조라고 해 봅시다. 삼각 격자가 있을 수 있고, 사각 격자도 있을 수 있겠죠. 이때 사각 격자라면 90도로 돌리면 원래로 돌아온다고 이해할 수 있어요. 삼각 격자는 120도 돌리면 돌아올 거고요. 이러한 대칭성을 쭉 분류해서 나온 2차원 격자 구조의 개수가 17개입니다. 3차원의 격자 구조는 훨씬 복잡합니다. 계산하면 총 230개가 나와요. 결론적으로 어떤 물질이건 이중 하나의 격자 구조를 갖습니다.”

전자의 스핀이란?
자, 이제 이러한 격자 구조 안에서 전자가 어떻게 돌아다니는지를 본격적으로 살펴보겠습니다. 인류는, 물리학은 지금 어디까지 도달해 있을까요? 머릿속에 현미경을 하나 마련하고, 점점 더 확대를 해보세요. 아니, 거기서 멈추지 말고 조금 더, 더, 확대를 해 보면 이성빈 교수님의 이야기가 조금은 실감 날 겁니다.

“격자 상의 전자를 볼게요. 이 격자 간 거리는 10의 -10제곱 미터입니다. 아주 작은 물질이라 하더라도 그 안에 무수히 많은 격자 구조가 있는 셈이죠. 또 무수히 많은 전자가 있을 거고요. 그렇기 때문에 전자들이 어떻게 상호 작용하는지, 어떻게 움직이는지를 ‘정확하게’ 푼다는 것은 불가능합니다. 만약 이것을 정확하게 풀 수 있다면 아무런 문제가 없겠죠. 물론 하나의 전자, 가령 수소는 정확하게 풀 수 있지만요. 아래 수식은 그 자체가 양자 역학의 시초가 되는 것인데요. 아직까지 우리는 이 수식을 절대 못 풀어요. 만약 이걸 풀면 모든 것을 다 알 수 있게 될 겁니다.”

그렇다면 어떻게 해야 하는가? 물리학자들은 포기하지 않고 다른 방법을 연구했습니다. 이때 물리학자들에게 아이디어가 된 것은 “격자의 주기성(periodicity)”을 살피는 일이었습니다.
“가령 사각 격자 구조를 갖는다고 한다면, 한 점에서 다른 점으로 이동해도 같은 구조가 반복될 겁니다. 그런 의미에서 격자 상에는 항상 주기성이라는 것이 존재하죠. 전자는 양자 역학에서 얘기하듯 파동 함수로 나타내는데요. 이 파동 함수가 주기성을 가지는 파동 함수 즉, ‘블로흐파’일 경우에 어떤 식으로 풀 수 있을지 살펴볼게요. 먼저 파동이 있고요. 이 파동은 파장을 갖습니다. 파장은 파동이 한 번 칠 때의 거리를 의미하는데요. ‘파수 벡터’는 파장에 반비례하는 (파장)⁻¹로 이해하시면 되고요. 이러한 파수 벡터가 정해지면 블로흐파가 정해집니다. 이때 우리는 그 파동 함수가 가지는 에너지를 구할 수 있습니다.”

이성빈 교수님은 전자의 블로흐파가 파동 함수의 에너지를 구하는 과정을 수식으로 보여 주며 “격자의 주기성 덕분에 우리는 격자에서 돌아다니는 전자의 파동 함수 또한 파수 벡터 공간에서 주기성을 갖는다고 이해할 수 있다.”라는 점을 설명했습니다. 다시 말해 실제 공간에서 격자가 주기성을 갖고 있고, 따라서 파장의 역(逆)에 해당하는 파수 벡터 역시 주기성을 갖고 있다는 것입니다. “그렇다면 각자 다른 파수 벡터에 따라 에너지가 어떻게 되는가를 계산할 수 있다.”는 이성빈 교수님은 아래의 표를 보여 주며 설명을 이어 갔습니다.
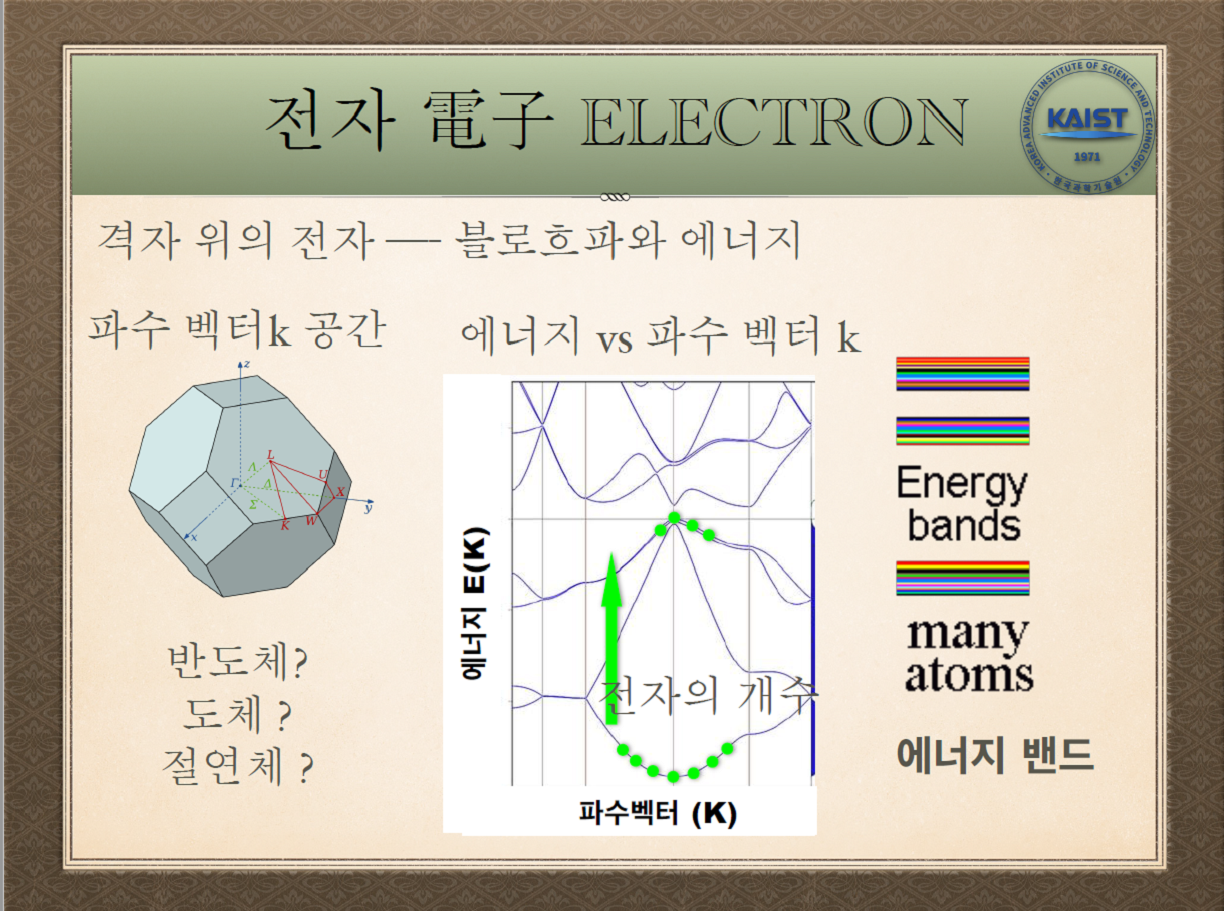
“이 스파게티처럼 생긴 선(웃음)은 각 파수 벡터에서 가질 수 있는 에너지값입니다. 즉 빈공간에 있는 에너지 파수에서는 전자가 흐를 수 없습니다. 존재할 수 없는 거죠. 이제 여기에 전자를 점점 채워가 볼게요. 전자의 개수에 따라 중간까지 채우거나 위까지 채울 수도 있어요. 파수 벡터와 에너지의 상관 관계에 있는 이 스파게티 같은 모양을 ‘에너지 밴드’라고 하는데요. 이것이 반도체의 모든 시초가 됩니다.”
좀 더 자세히 들여다볼까요. 앞서 이성빈 교수님은 전자는 언제나 에너지 밴드 위에서만 존재할 수 있다고 설명했습니다. 한편 에너지 밴드와 에너지 밴드 사이에는 틈이 있는데 이 틈을 ‘에너지 틈’이라고 부릅니다. 이 빈 공간에서는 어떠한 상태도 존재할 수 없습니다. 만약 전자의 개수를 계속 채우다가 에너지 틈 바로 아래까지 전자의 개수를 모두 채웠다면 이 경우 더 이상 전기 자극에 반응하지 않겠죠. 이것이 ‘절연체’입니다.
격자의 주기성을 이용해 전자들이 어떻게 상호 작용하는지, 어떻게 움직이는지를 살짝 엿보았지만 안타깝게도, 우리는 정확한 답은 여전히 구하지 못했습니다.
위상 절연체의 발견
아직 인류가 도달하지 못한 영역에 대한 아쉬움은 잠깐 뒤에 이야기하도록 하겠습니다. 이성빈 교수님은 현대 물리학의 발견들, 그러니까 노벨 물리학상 수상 장면을 잠시 살펴보았습니다. 앞서 이야기했듯 그래핀을 발견해 2010년 노벨 물리학상을 수상한 가임과 노보셀로프에 이어 이성빈 교수님이 소개한 물리학의 발견은 ‘위상 절연체(Topological Insulator)’의 발견이었습니다.
“앞서 에너지 밴드 이야기를 했죠. 위상 절연체란 에너지 틈까지 전자를 쭉 채워서 보니 가장자리에서만 에너지 틈이 없는 다른 종류의 절연체였다는 거예요. 분명히 절연체인데 표면에서만 흐르는 뭔가가 있다면 그것은 우리가 알던 절연체와는 다른 거죠. 던컨 홀데인(Duncan Haldane)과 마이클 코스털리츠(Michael Kosterlitz)가 2016년 이 위상학적 양자 상의 발견으로 노벨 물리학상을 수상했습니다.”
물리학에서 위상학적 양자 상의 발견은 무엇을 의미할까요? 더 자세히 살펴보기 위해 이성빈 교수님은 위상 수학의 ‘가우스-보넷 이론’에 대한 설명을 이어 갑니다.

“돌고래든, 공이든, 소든 표면 곡률의 합은 항상 일정하다는 것이 가우스-보넷 이론입니다. 어떻게 생겼든 상관없어요. 이때 구멍이 있으면 안 되는데요. 하지만 구멍의 개수에 따라서도 같은 값이 나옵니다. 구멍이 한 개 있으면 곡률의 합은 또 같고, 두 개 있는 것들끼리 또한 같은 겁니다. 아주 쉽죠? (웃음) ‘표면 곡률의 합은 항상 일정하다.’라는 말을 조금 철학적으로 생각해 보자면 ‘환원주의(reductionism)’에 해당하는 건데요. 디테일은 상관하지 않고 빵에 구멍이 몇 개 있는지만 알면 된다는 겁니다. 이것이 위상 수학의 핵심입니다.”
물리학자들은 이 개념을 물리학으로 가져왔습니다. ‘양자홀 효과(Quantum Hall Effect)’는 시료면에 전류를 흘려보내고, 다시 그것과 수직으로 강한 전류 자기장을 걸었을 때 양자에 수직인 방향으로 전장이 생기는데 이때 측정한 값이 신기하게도 언제나 정수배가 되는 현상을 말합니다.

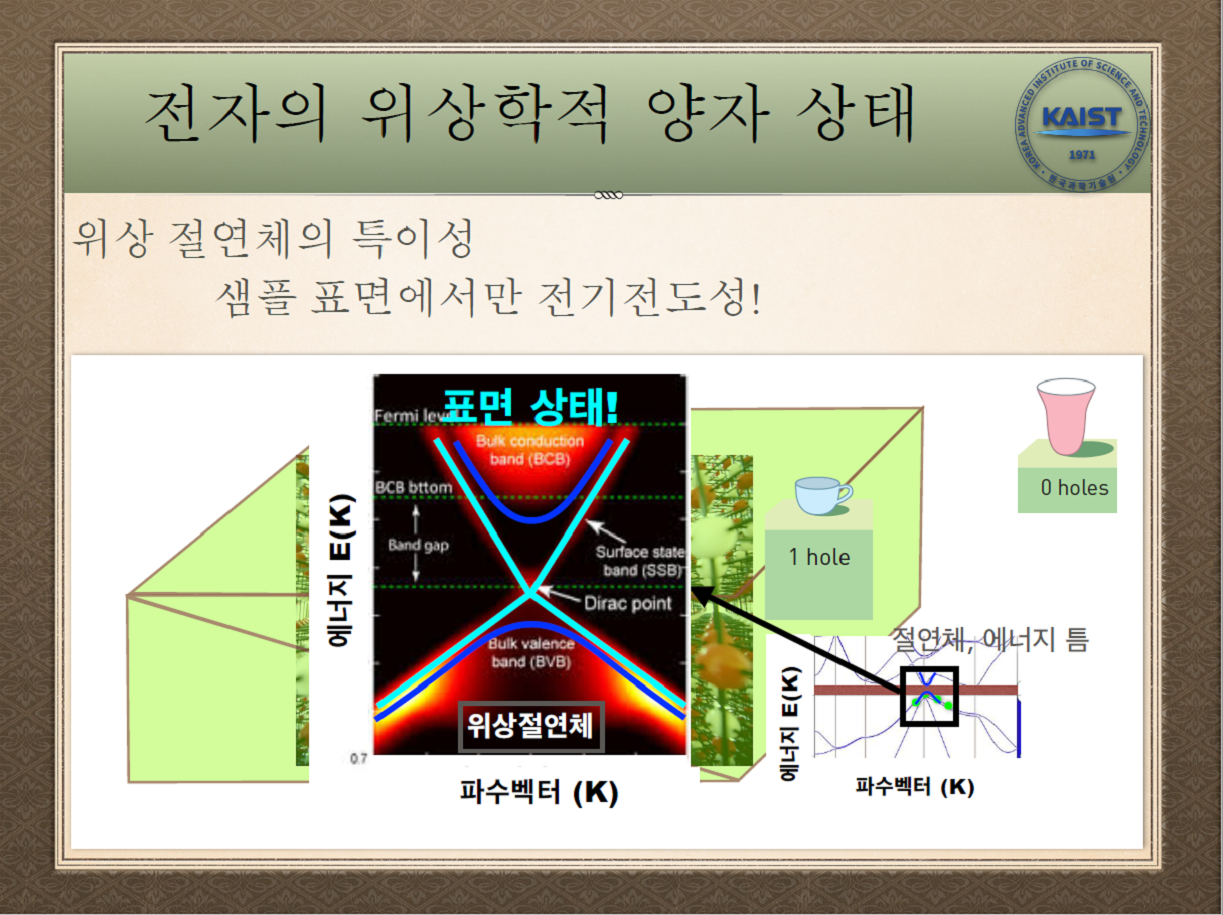
“샘플이 어떻게 생겼건 상관없이 전류를 흘리고, 자기장을 걸었을 때 그 자기장 세기에 따라 결과가 항상 정수배로 층층이 나온다는 거예요. 이건 그동안 배운 절연체와는 또 다르죠. 위상 절연체는 실제로는 샘플 표면에서만 전기 전도성을 갖는데요. 이것을 구멍이 하나도 없는 시스템이라고 한다면 격자 안에서는 마치 진공 상태와는 다른 파동 함수를 가져서 구멍이 하나 있는 시스템을 가질 수 있는 거예요. 앞서 본 에너지 밴드에서 위상 절연체는 표면에 무언가가 있어서, 절연체이면서도 에너지 틈 사이에서 표면 상태로 나오는 겁니다. 이것은 실험으로 직접 에너지 밴드 모양을 측정할 수가 있어요. 이것 역시 아주 대단한 실험입니다.”
(2편에서 계속)
「물리 어벤져스 2019」
2강 “지구인으로 살아가기: 우주 날씨와 인공 위성”
「물리 어벤져스 2019」 2강 “지구인으로 살아가기: 우주 날씨와 인공 위성”은 7월 26일 금요일 7시 30분에 ‘민음사 본사 지하 2층 이벤트홀’에서 진행됩니다.

오시는 길▼
◆ 함께 읽으면 좋은 책들 ◆



'완결된 연재 > (完) 물리 어벤져스 2019 스케치' 카테고리의 다른 글
| 3강 금속이 액체라면? 임혜인 숙명여대 교수 2편 (0) | 2019.10.16 |
|---|---|
| 3강 금속이 액체라면? 임혜인 숙명여대 교수 1편 (0) | 2019.10.11 |
| 2강 지구인으로 살아가기: 황정아 박사 2편 (0) | 2019.09.10 |
| 2강 지구인으로 살아가기: 황정아 박사 1편 (0) | 2019.09.03 |
| 1강 혼돈의 양자 스핀: 이성빈 카이스트 교수 2편 (0) | 2019.07.03 |




